A.2 Neurodesarrollo del Lenguaje Matemático mediante ¡Me Gusta Matemática!
_(2).png)
¿Cuáles son las competencias cognitivas básicas del Lenguaje Matemático?
En el proceso de construcción de conocimiento de un estudiante, sabemos que primero deberemos desarrollar las Funciones Cognitivas Básicas que estarán relacionadas con los Procesos Cogntivios Específicos, y que luego formarán parte de la construcción de los Procesos/Competencias Cognitivas Superiores. Es decir, se pueden considerar que estas competencias cognitivas básicas son un prerrequisito necesario para que cada estudiante pueda lograr alcanzar el Neurodesarrollo Competencial Óptimo del Lenguaje Matemático.
Las competencias cognitivas básicas son las siguientes:
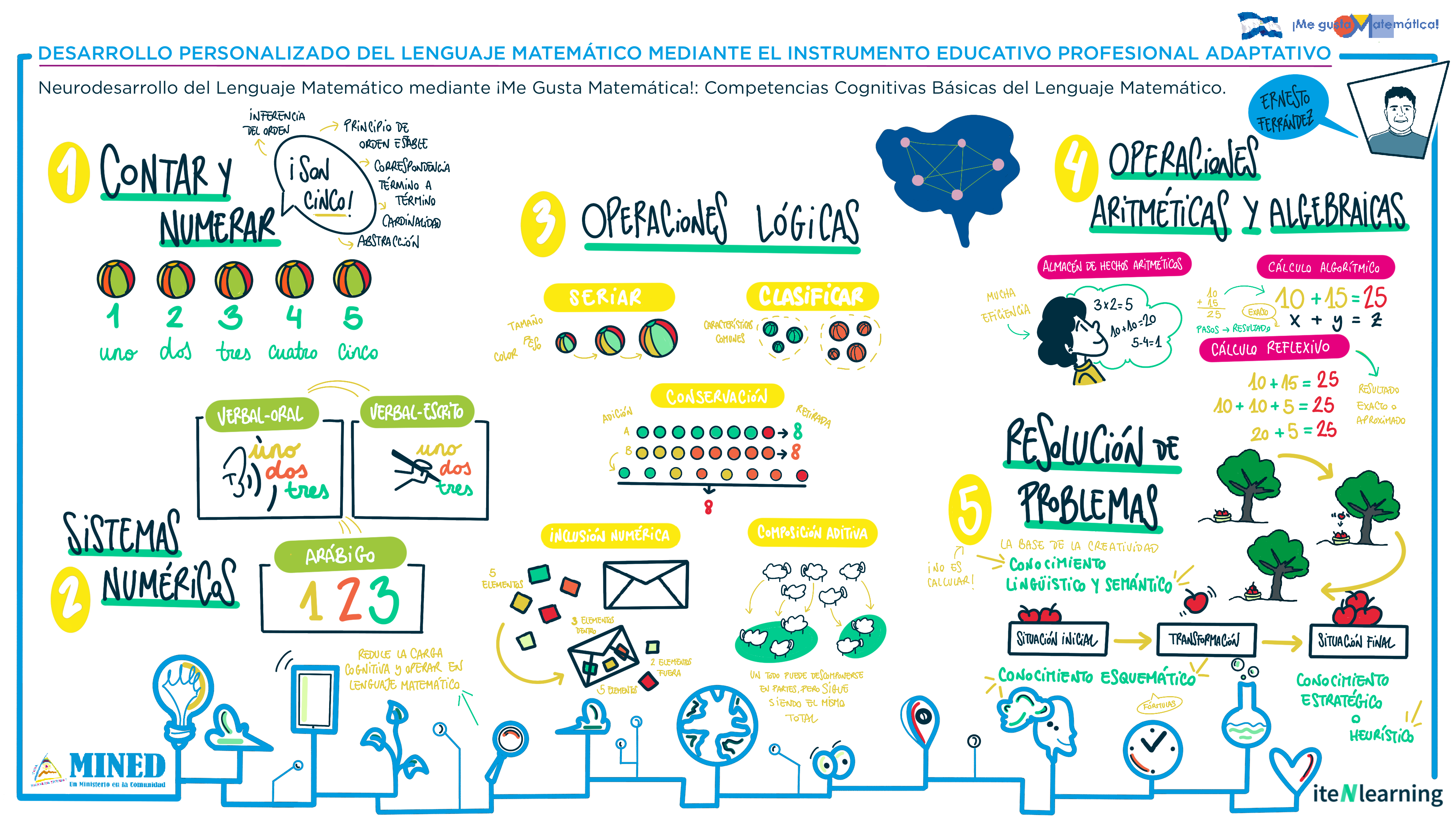
1. Contar y Numerar
- Contar es la capacidad de recitar una lista de palabras que designan un número
- Numerar es la capacidad de determinar el cardinal de un conjunto
Esta competencia cognitiva supone una serie de principios que deben estar adquiridos:
- Principio de orden estable
- Principio de correspondencia término a término
- Principio cardinal
- Principio de la inferencia del orden
- Principio de abstracción
2. Sistemas numéricos tienen Modelos Neuropsicológicos que nos permiten entenderlos. Podemos diferenciar dos:
- Verbal Oral y Verbal Escrito: hacen de puente entre el Lenguaje Verbal y el Lenguaje Matemático
- Arábigo: sistema numérico diseñado para reducir la carga cognitiva y que nos permita representar el Lenguaje Matemático
3. Operaciones Lógicas, diferenciamos:
- Seriación: ordenar objetos a partir de sus diferencias
- Clasificar: agrupar objetos en conjuntos comunes prestando atención únicamente a sus características comunes
- Conversación numérica: integramos la seriación y la clasificación. Significa que el número de objetos que existe en un conjunto sólo puede modificarse mediante la adición o retirada de uno o varios de sus elementos
- Inclusión numérica: los números se comportan como conjuntos que se embeben unos a otros.
- Composición aditiva: partiendo del principio de inclusión numérica, un todo puede descomponerse en partes. Un total que se divide sigue siendo el mismo total.
Estas 5 operaciones lógicas son la base en las que se sustenta la capacidad lógica de un estudiante.
4. Operaciones Aritméticas (trabajamos con números y signos) y Algebraicas (trabajamos con letras), pueden resolverse de diversas formas:
- Almacén de hechos aritméticos. Es importante que nuestro estudiante desarrollen un buen almacén de hechos aritméticos ya que nos ayuda a reducir la carga cognitiva
- Cálculo algorítmico: calculamos mediante un conjunto de pasos o procesos con el fin de conseguir un resultado exacto.
- Cálculo Reflexivo (o mental): se basa en aplicar el conjunto de propiedades de la matemática con el fin de conseguir un resultado exacto o aproximado.
5. Resolución de problemas aritméticos, es decir, problemas en los que trabajamos con números y signos. Esta competencia es la base de la capacidad de creatividad: de hallar, de inventar… De lo que los matemáticos llaman Heurística.
Cuando hablamos de Resolución de Problemas no hablamos de calcular, el cálculo es un paso final para hallar la solución del problema. Sino que esta competencia se basa en que seamos capaces de pasar de Lenguaje Verbal (es decir de la historia del problema) al Lenguaje Matemático. Y que el estudiante sea capaz de operar en este Lenguaje Matemático. Para ello se necesitan varios niveles de conocimiento:
- Conocimiento lingüístico
- Conocimiento semántico
- Conocimiento esquemático (el cerebro tiene un esquema estructurado que reconoce y trabaja con él). Por ejemplo, en un problema de cambio el estudiante debe ser capaz de reconocer la estructura del mismo: Situación Inicial, Transformación y Situación Final
- Conocimiento estratégico o heurístico, es decir, ser capaces de construir soluciones, hallar e inventar
Nos tenemos que asegurar que los estudiantes, cuando estén desarrollando la capacidad de resolución de problemas, sea capaz de hallar la estructura del mismo. Lo importante no es que responda con la solución esperada.
Los Instrumentos Educativos Profesionales como ¡Me Gusta Matemática! tienen en cuenta los procesos de construcción de estas competencias cognitivas básicas y trabajan con el estudiante de manera adaptada con el fin de asegurar su desarrollo adecuado.
Pero hay un paso más, una vez los estudiantes han logrado desarrollar estas competencias básicas, hemos de asegurar que continúen desarrollando los Procesos Cognitivos necesarios para alcanzar su Neurodesarrollo Competencial Óptimo. Para ello, sabemos que hay unas Funciones Cognitivas asociadas a unos Procesos Cognitivos Específicos que pueden ser del Lenguaje Verbal o Lenguaje Matemático, y unos Procesos Cognitivos Superiores.
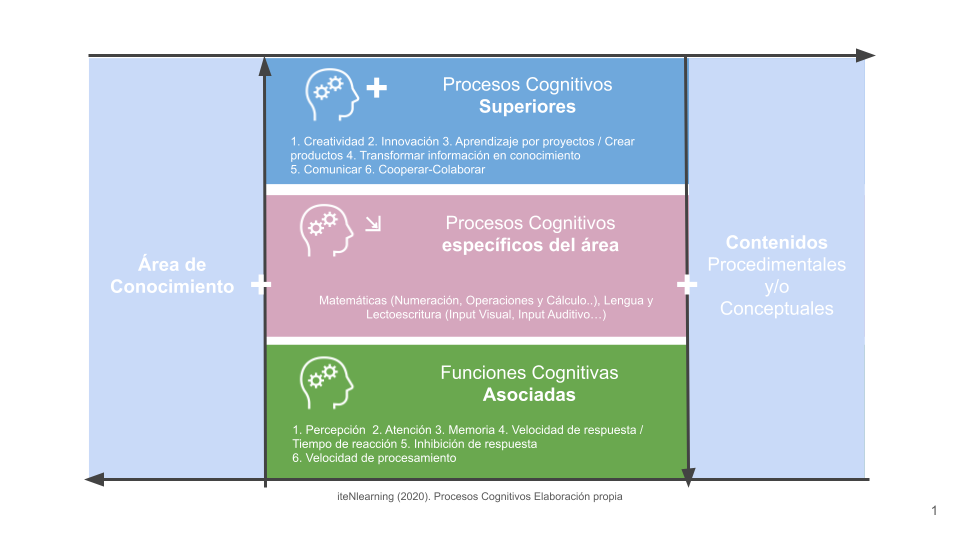
Si nos centramos en el desarrollo del Lenguaje Matemático,
- Debemos saber que es un Lenguaje Matemático distinto al Lenguaje Verbal
- Alcanzar la capacidad de Codificación (pasar del Lenguaje Verbal al Lenguaje Matemático), reduciendo la carga cognitiva y permitiendo a los estudiantes llegar a alcanzar un primer nivel de abstracción.
- Alcanzar la capacidad de Resolución de Problemas Aritméticos que los matemáticos llaman heurística y permite a los estudiantes llegar a ser capaces de hallar, inventar… (primer paso de la creatividad matemática)
Con estos elementos se produce la capacidad de operar lógicamente con ellos. Desarrollando los Procesos Cognitivos Específicos del área de Matemáticas:
- Numerar y Contar
- Operaciones Lógicas
- Resolución de Problemas aritméticos
Así como aquellos procesos con un componente conceptual:
- Geometría
- Unidades y Medidas
- Tratamiento de la Información
